Fast and accurate three-dimensional point spread function computation for fluorescence microscopy

Abstract

The point-spread function (PSF) plays a fundamental role in fluorescence microscopy. A realistic and accurately calculated PSF model can significantly improve the performance in 3D deconvolution microscopy and also the localization accuracy in single-molecule microscopy. In this work, we propose a fast and accurate approximation of the Gibson-Lanni model, which has been shown to represent the PSF suitably under a variety of imaging conditions. We express the Kirchhoff’s integral in this model as a linear combination of rescaled Bessel functions, thus providing an integral-free way for the calculation. The explicit approximation error in terms of parameters is given numerically. Experiments demonstrate that the proposed approach results in a significantly smaller computational time compared with current state-of-the-art techniques to achieve the same accuracy. This approach can also be extended to other microscopy PSF models.

Key points

• We express the integral in this model as a linear combination of rescaled Bessel functions, providing an integral-free way for the calculation.
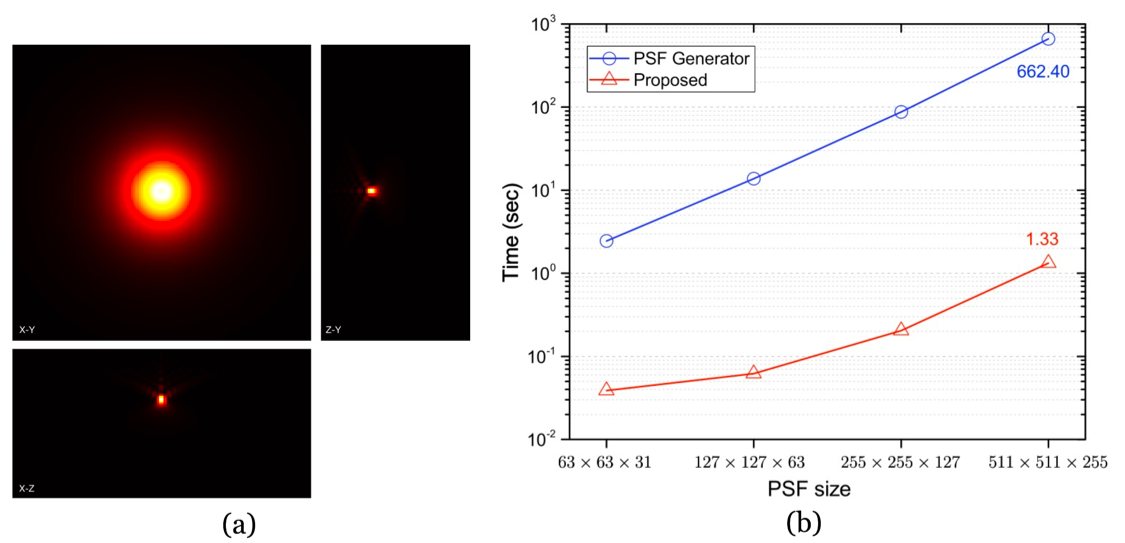
• Experiments demonstrate that the proposed approach results in significantly smaller computational time compared with the quadrature approach (e.g. PSF Generator¹).
• This approach can also be extended to other microscopy PSF models.

The Gibson-Lanni Model ²

This model is based on a calculation of the optical path difference (OPD) between the design conditions and experimental conditions of the objective. It accounts for coverslips and other interfaces between the specimen and the objective.

$$ OPD(\rho,\mathrm{z}; z_p, {\boldsymbol \tau}) = (\mathrm{z} + t_i^* )\sqrt{n_i^2 - (\mathrm{NA}\rho)^2}+ z_p\sqrt{n_s^2 - (\mathrm{NA}\rho)^2} - t_i^* \sqrt{(n_i^*)^2 - (\mathrm{NA}\rho)^2} + t_g \sqrt{n_g^2 - (\mathrm{NA}\rho)^2 } - t_g^{*}\sqrt{(n_g^{*})^2 - (\mathrm{NA}\rho)^2}, $$

where \(\rho\) is the normalized radius in the focal plane, \(\mathrm{z}\) is the axial coordinate of the focal plane, \(z_p\) is the axial location of the point-source in the specimen layer relative to the cover slip and \(\mathbf{p}=(\mathrm{NA}, \mathrm{n}, \mathrm{t})\) is a parameter vector containing the physical parameters of the optical system: \(\mathrm{NA}\) is the numerical aperture, \(\mathrm{n}\) represents the refractive index and \(\mathrm{t}\) is the thickness of individual layers.

The Gibson-Lanni model is expressed by $$ \mathrm{PSF}(\mathrm{r}, \mathrm{z}; z_p, \mathbf{p}) = \left|A\int_0^a e^{iW(\rho,\mathrm{z}; z_p, \mathbf{p})} J_0\left(k\mathrm{r}\mathrm{NA}\rho\right) \rho \mathrm{d}\rho\right|^2 $$ where the phase term \(W(\rho,\mathrm{z}; z_p, \mathbf{p})=k,OPD(\rho,\mathrm{z}; z_p, \mathbf{p})\), \(k=2\pi/\lambda\) is the wave number of the emitted light. \(A\) is a constant complex amplitude, and \(J_0\) denotes the Bessel function of the first kind of order zero.

Bessel Series Approximation

The main idea is based on the fact that the integral \(\int_{0}^{\alpha}tJ_0(ut)J_0(vt)dt\) can be explicitly computed as ³ $$ \int_0^a t J_0(ut)J_0(vt) dt = a\Big(\frac{uJ_1(ua)J_0(va) - v J_0(ua)J_1(va)}{u^2-v^2}\Big). $$

If we expand the function \(e^{iW(\rho,\mathrm{z}; z_p, \mathbf{p})}\) as a linear combination of rescaled Bessel function and fit the coefficients, then $$ \mathrm{PSF}_{\mathrm{app}}(\mathrm{r}, \mathrm{z}; z_p, \mathbf{p}) = \left|A\sum_{m=1}^{M}c_m (\mathrm{z}) R_m(\mathrm{r}; \mathbf{p})\right|^2, \mathrm{where\ }R_m(\mathrm{r}; \mathbf{p})=\frac{\sigma_mJ_1(\sigma_ma)J_0(\eta a)a - \eta J_0(\sigma_ma)J_1(\eta a)a}{\sigma_m^2 - \eta^2}. $$

Compared with PSFGenerator¹

Software

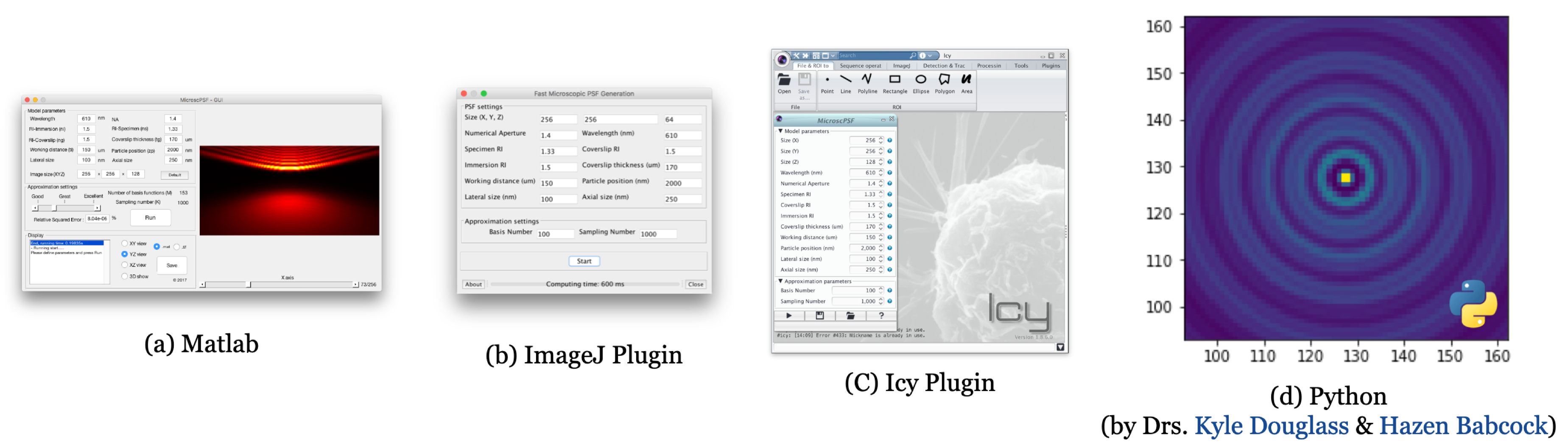
Call the PSF generation from the ImageJ-Ops

See more here.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import net.imagej.ops.AbstractOpTest;
import net.imglib2.Dimensions;
import net.imglib2.FinalDimensions;
import net.imglib2.img.Img;
import net.imglib2.type.numeric.real.DoubleType;


double NA = 1.4; // numerical aperture
double lambda = 610E-09; // wavelength
double ns = 1.33; // specimen refractive index
double ni = 1.5; // immersion refractive index, experimental
double resLateral = 100E-9; // lateral pixel size
double resAxial = 250E-9; // axial pixel size
double pZ = 2000E-9D; // position of particle


DoubleType type = new DoubleType(); // pixel type of created kernel
Dimensions dims = new FinalDimensions(256, 256); //dimensions


Img<DoubleType> kernel = ops.create().kernelDiffraction(dims, NA, lambda, ns, ni, resLateral, resAxial, pZ, type);

Extensions

Non-cylindrically symmetric PSF generation (e.g. with coma, astigmatism aberrations represented in vectorial models)?

In principle, the proposed approach can be extended to those cases, provided other models are able to be expressed in the form of Kirchhoff’s integral formula. Haeberle⁴ showed that the vectorial model can also be combined with the ease of use of the Gibson-Lanni scalar approach, which has the advantage of introducing explicitly the known or sample-dependent parameters.

Here is a sample code which supports angle-dependent PSF generation.

PSF Engineering (e.g. double-helix PSF)?

It maybe interesting in some sense to include the spherical aberration in the double-helix PSF, see⁵ for the discussion.

Applications

See citations, more examples to be added.

• 3D deconvolution microscopy by PURE-LET and 3D microscopy PSF estimation
• Cytokit: A single-cell analysis toolkit for high dimensional fluorescent microscopy imaging
• Flowdec: TensorFlow Deconvolution for Microscopy Data